Quantum linear system algorithm with optimal queries to initial state preparation

Abstract

The quantum linear system problem provides one of the most enticing sources of exponential quantum speedups, and its resolution underlies other interesting quantum algorithms for differential equations and eigenvalue processing. The goal is to produce a state proportional to the solution $A^{-1}|b\rangle$ of a linear system with accuracy $\epsilon$, by querying an oracle $O_A$ that block encodes the coefficient matrix and an oracle $O_b$ that prepares the initial state.

We present a quantum linear system algorithm with query complexity $\mathbf{\Theta}\left(1/\sqrt{p}\right)$ to $O_b$ that is optimal, and query complexity $\mathbf{O}\left(\kappa\log\left(1/p\right)\left(\log\log\left(1/p\right)+\log\left({1}/{\epsilon}\right)\right)\right)$ to $O_A$ that is nearly optimal in all parameters including the condition number $\kappa=\Vert A\Vert\Vert A^{-1}\Vert$ and success amplitude $\sqrt{p}={\Vert A^{-1}|b\rangle\Vert}/{\Vert A^{-1}\Vert}$. In various applications to solving differential equations, preparing ground states of operators with real spectra, estimating and transforming eigenvalues of non-normal matrices, we can further improve the dependence on $p$ to nearly match or outperform best previous results based on other methods. As $\kappa$ can be arbitrarily larger than $1/\sqrt{p}$, our algorithm contrasts with recent results that have $\mathbf{O}\left(\kappa\log\left({1}/{\epsilon}\right)\right)$ complexity to both oracles, which, while optimal in $O_A$, is highly suboptimal in $O_b$.

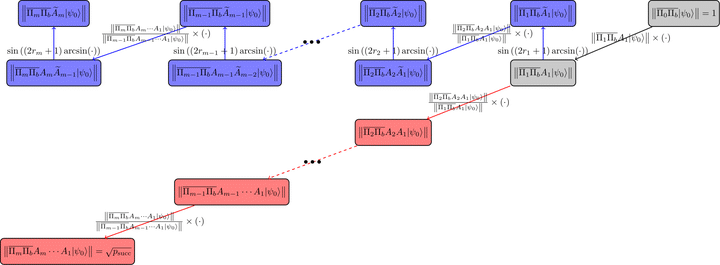
We achieve this by a new Variable Time Amplitude Amplification algorithm with Tunable thresholds (Tunable VTAA), which fully characterizes generic nested amplitude amplifications, eliminates redundant nestings, and is of independent interest. With an optimized schedule of thresholds, we prove that the complexity of Tunable VTAA scales with $\ell_{\frac{2}{3}}$-quasinorm of the input costs, improving over the $\ell_1$-norm result of Ambainis and the more common $\ell_2$-norm scaling. Specialized to the quantum linear system problem, we construct a discretized inverse state, for which a deterministic amplification schedule exists. This leads to a substantially simplified VTAA with an optimal initial state preparation cost, even when the solution norm is not known $\textit{a priori}$.

We also introduce a block preconditioning scheme that can artificially boost $\sqrt{p}$ in generic situations, in contrast to previous negative preconditioning results focusing on reducing $\kappa$. This further reduces the cost of initial state preparation in linear-system-based differential equation solvers, ground state preparators and eigenvalue processors. Additionally, block preconditioning furnishes a particularly simple quantum linear system algorithm with optimal $\mathbf{O}\left(\kappa\log\left(\frac{1}{\epsilon}\right)\right)$ queries to $O_A$ by using $|b\rangle$ itself as the preconditioner. It also realizes a block-encoded eigenvalue transformer with $\mathbf{O}(n)$ scaling in degree of the target polynomial, compared to the best existing result of $\mathbf{O}\left(n^{1.5}\right)$.