Quantum eigenvalue processing

Abstract

Many problems in linear algebra require processing eigenvalues of the input matrices. As eigenvalues are different from singular values for non-normal operators, these problems are out of reach of the existing quantum singular value algorithm and its descendants.

We present a Quantum EigenValue Estimation (QEVE) algorithm and a Quantum EigenValue Transformation (QEVT) algorithm that estimate and transform eigenvalues of high-dimensional matrices accessed by a quantum computer through block encoding oracles. We focus on input matrices with real spectra and Jordan forms—a broad class of operators that can describe non-Hermitian physics and transcorrelated quantum chemistry. However, our technique also handles general non-normal matrices with complex eigenvalues, and our method remains efficient even when the Jordan basis is ill conditioned.

Our QEVE estimates an eigenvalue of a diagonalizable matrix using $\mathbf{O}\left(\alpha\kappa/\epsilon\log(1/p)\right)$ queries to its block encoding and a unitary preparing the corresponding eigenstate, in terms of error $\epsilon$, failure probability $p$, normalization factor $\alpha$ of the block encoding, and condition number $\kappa$ of its basis transformation. This solves the eigenvalue estimation problem for a broad class of non-normal matrices with the Heisenberg-limited scaling, which naturally reduces to the optimal estimation of singular values that has long been known. Our approach is conceptually simple, based on reductions to the optimal scaling quantum linear system algorithm, improving over prior approaches using differential equation solvers which are polylogarithmic away from optimum.

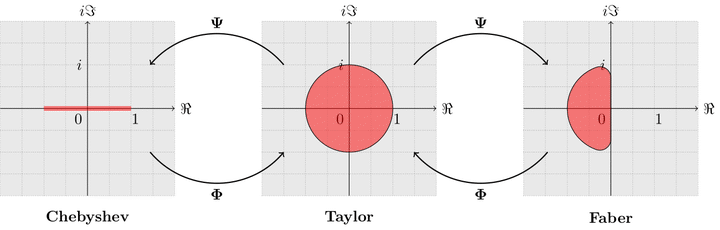
Our QEVT implements transformations on eigenvalues of the input matrix through the Chebyshev and Faber approximations. As these expansions provide a close-to-best uniform polynomial approximation of functions over the complex plane, the query complexity of QEVT is expected to be nearly optimal. In particular, our eigenvalue algorithm achieves a performance comparable to previous singular value transformation results for the special case of Hermitian inputs, where eigenvalues coincide with singular values in magnitude.

As an application, we present a quantum differential equation algorithm based on QEVT, whose query complexity scales strictly linear in the evolution time $t$ for an average-case diagonalizable input with imaginary spectra, whereas the best previous approach has a complexity with an extra multiplicative $\mathrm{polylog}(t)$ factor. We also develop a quantum algorithm for preparing the ground state of matrices with real spectra, which reduces to the nearly optimal result for Hermitian Hamiltonians from previous work.

Underlying both QEVE and QEVT is an efficient quantum algorithm for preparing the Chebyshev history state through its matrix generating function, encoding Chebyshev polynomials of the input matrix in quantum superposition, which may be of independent interest. Prior to our work, it was known how to efficiently create such a state only for Hermitian inputs. We then extend this result to prepare the Faber history state, achieving efficient eigenvalue transformation over the complex plane. Independently, we develop techniques to generate $n$ Fourier coefficients using $\mathbf{O}(\mathrm{polylog}(n))$ gates, improving over prior approaches with a cost of $\mathbf{\Theta}(n)$.

Our result thus provides a unifying framework for processing eigenvalues of matrices on a quantum computer.