Time-dependent Hamiltonian simulation with $L^1$-norm scaling

Abstract

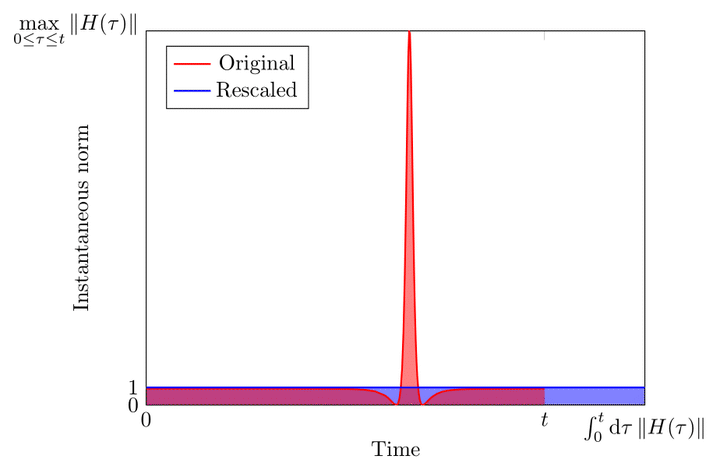
The difficulty of simulating quantum dynamics depends on the norm of the Hamiltonian. When the Hamiltonian varies with time, the simulation complexity should only depend on this quantity instantaneously. We develop quantum simulation algorithms that exploit this intuition. For sparse Hamiltonian simulation, the gate complexity scales with the $L^1$ norm $\int_{0}^{t}\mathrm{d}\tau\Vert H(\tau)\Vert_{\max}$, whereas the best previous results scale with $t\max_{\tau\in[0,t]}\Vert H(\tau)\Vert_{\max}$. We also show analogous results for Hamiltonians that are linear combinations of unitaries. Our approaches thus provide an improvement over previous simulation algorithms that can be substantial when the Hamiltonian varies significantly. We introduce two new techniques: a classical sampler of time-dependent Hamiltonians and a rescaling principle for the Schr"{o}dinger equation. The rescaled Dyson-series algorithm is nearly optimal with respect to all parameters of interest, whereas the sampling-based approach is easier to realize for near-term simulation. These algorithms could potentially be applied to semi-classical simulations of scattering processes in quantum chemistry.